初心者向けプログラミング講座
第8回: 測定データの応用処理とレポート作成

講座の概要については以下からご覧ください。
目的
この回では、測定データのより高度な処理と、その結果をレポートとしてまとめる方法を学びます。具体的には、Pythonを活用して測定データの応用処理を行う方法(フィッティングや統計処理など)と、結果をCSVやPDF形式で出力するフローを習得します。これにより、他者にわかりやすく分析結果を報告できるスキルを身につけます。
学習内容
- 高度なデータ処理(データフィッティング、統計処理)
- 測定データの保存と書式設定(CSV形式の応用)
- PDF形式のレポート作成
- 実践プログラム例
- 演習問題
1. 高度なデータ処理
測定データの応用処理として、代表的なタスクである「データフィッティング」と「統計処理」について学びます。
(1) データフィッティング
フィッティングとは、測定データに数式モデルを適合させ、その背後にある関係性を明らかにする手法です。Pythonのライブラリscipyを使うと、非線形モデルのフィッティングも簡単に行えます。
例:サイン波へのフィッティング
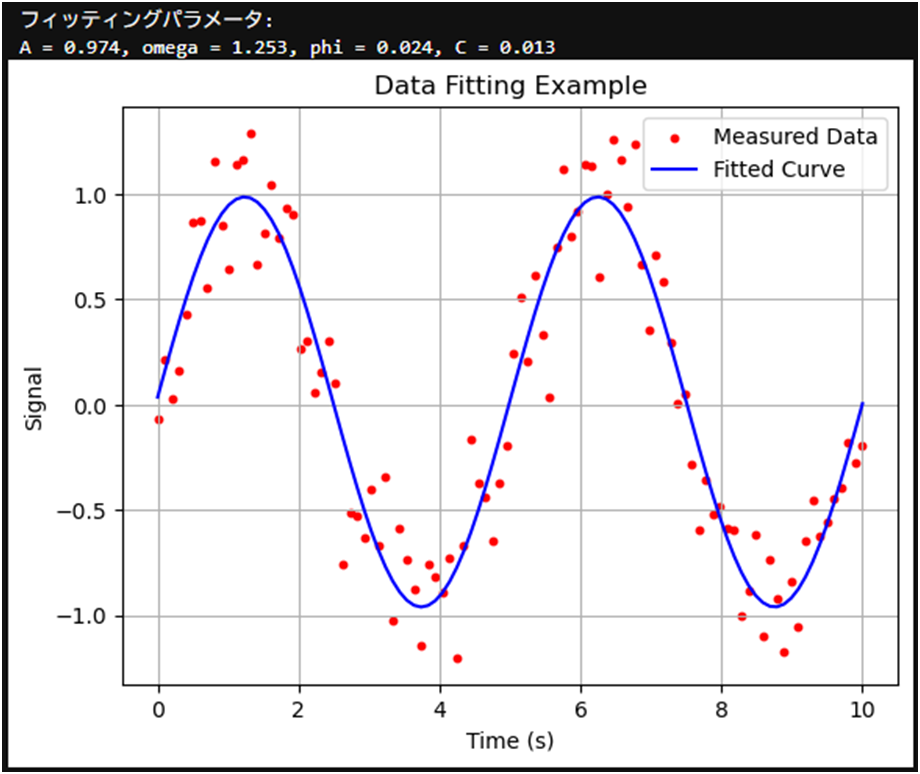
以下では、測定データをサイン波モデルでフィッティングする例を示します。
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
# ダミーデータ(信号+ノイズ)
x = np.linspace(0, 10, 100)
y = np.sin(2 * np.pi * x / 5) + 0.2 * np.random.normal(size=100)
# モデル関数(サイン波)
def sine_model(x, A, omega, phi, C):
return A * np.sin(omega * x + phi) + C
# フィッティングの実行
params, covariance = curve_fit(sine_model, x, y, p0=[1, 2 * np.pi / 5, 0, 0]) # 初期値を指定
A, omega, phi, C = params # フィッティング結果のパラメータ
# フィッティング結果を表示
print("フィッティングパラメータ:")
print(f"A = {A:.3f}, omega = {omega:.3f}, phi = {phi:.3f}, C = {C:.3f}")
# フィッティングしたモデルをプロット
plt.scatter(x, y, label="Measured Data", color="red", s=10) # 測定データ
plt.plot(x, sine_model(x, A, omega, phi, C), label="Fitted Curve", color="blue") # フィッティングカーブ
plt.title("Data Fitting Example")
plt.xlabel("Time (s)")
plt.ylabel("Signal")
plt.legend()
plt.grid()
plt.show()実行結果
(2) 統計処理
測定データセットの要約情報を求めるために、統計量(平均、標準偏差など)を利用します。Pythonのライブラリnumpyやscipy.statsを使うと簡単に実装可能です。
例:統計量の計算
import numpy as np
# 測定データ
data = [2.1, 2.3, 2.2, 2.5, 2.4, 2.3, 2.2]
# 基本統計量の計算
mean = np.mean(data) # 平均
std_dev = np.std(data) # 標準偏差
max_val = np.max(data) # 最大値
min_val = np.min(data) # 最小値
print("統計量:")
print(f"平均: {mean:.3f}, 標準偏差: {std_dev:.3f}, 最大値: {max_val:.3f}, 最小値: {min_val:.3f}")実行結果

2. 測定データの保存と書式設定
レポートを作成する際、測定データをCSV形式で保存し、それに追加情報(統計量や注釈など)を付加する場合があります。
(1) CSVへの保存(統計量を含む)
以下に、測定データとその統計量を保存する例を示します。
import csv
# 測定データ
data = [2.1, 2.3, 2.2, 2.5, 2.4, 2.3, 2.2]
# 統計量を計算
mean = np.mean(data)
std_dev = np.std(data)
# CSV保存
with open("measurement_results.csv", "w", newline="") as csvfile:
writer = csv.writer(csvfile)
writer.writerow(["Measurement", "統計量"])
for value in data:
writer.writerow([value])
writer.writerow([]) # 空行
writer.writerow(["Mean", mean])
writer.writerow(["Standard Deviation", std_dev])
print("データが measurement_results.csv に保存されました。")3. PDF形式のレポート作成
Pythonのfpdfライブラリを使えば、測定データや統計情報をPDF形式のレポートとして保存することができます。
(1) ライブラリのインストール
fpdfライブラリをインストールします。
pip install fpdf(2) PDFレポートの生成
以下に、測定結果と統計量をPDFレポートにまとめるサンプルコードを示します。
from fpdf import FPDF
# 測定データと統計量
data = [2.1, 2.3, 2.2, 2.5, 2.4, 2.3, 2.2]
mean = np.mean(data)
std_dev = np.std(data)
# PDFを作成
pdf = FPDF()
pdf.set_auto_page_break(auto=True, margin=15)
pdf.add_page()
# タイトル
pdf.set_font("Arial", size=16)
pdf.cell(200, 10, txt="Measurement Report", ln=True, align="C")
# 測定データ
pdf.set_font("Arial", size=12)
pdf.cell(200, 10, txt="Measurements:", ln=True)
for i, value in enumerate(data):
pdf.cell(200, 10, txt=f"Data Point {i+1}: {value:.3f}", ln=True)
# 統計結果
pdf.cell(200, 10, txt=f"Mean: {mean:.3f}", ln=True)
pdf.cell(200, 10, txt=f"Standard Deviation: {std_dev:.3f}", ln=True)
# ファイル保存
pdf.output("measurement_report.pdf")
print("レポートが measurement_report.pdf として保存されました。")4. 実践プログラム例
以下のプログラムでは、ダミーデータの取得、フィッティング、CSV保存、PDFレポート作成までの一連の処理を統合しています。
統合プログラム例
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
from fpdf import FPDF
import csv
# ダミーデータ生成
x = np.linspace(0, 10, 100)
y = np.sin(2 * np.pi * x / 5) + 0.2 * np.random.normal(size=len(x))
# --- フィッティング ---
def sine_model(x, A, omega, phi, C):
return A * np.sin(omega * x + phi) + C
params, _ = curve_fit(sine_model, x, y, p0=[1, 2 * np.pi / 5, 0, 0])
A, omega, phi, C = params
# --- グラフの作成 ---
plt.scatter(x, y, label="Measured Data", color="red", s=10)
plt.plot(x, sine_model(x, A, omega, phi, C), label="Fitted Curve", color="blue")
plt.title("Measurement and Fitting")
plt.xlabel("Time (s)")
plt.ylabel("Signal")
plt.legend()
plt.grid()
plt.savefig("measurement_plot.png")
plt.show()
# --- 統計量計算 ---
mean = np.mean(y)
std_dev = np.std(y)
# --- CSV保存 ---
with open("results.csv", "w", newline="") as csvfile:
writer = csv.writer(csvfile)
writer.writerow(["X", "Y"])
for xi, yi in zip(x, y):
writer.writerow([xi, yi])
writer.writerow([])
writer.writerow(["Mean", mean])
writer.writerow(["Standard Deviation", std_dev])
# --- PDFレポート作成 ---
pdf = FPDF()
pdf.add_page()
pdf.set_font("Arial", size=16)
pdf.cell(200, 10, txt="Measurement Report", ln=True, align="C")
pdf.set_font("Arial", size=12)
pdf.cell(200, 10, txt=f"Mean: {mean:.3f}", ln=True)
pdf.cell(200, 10, txt=f"Standard Deviation: {std_dev:.3f}", ln=True)
pdf.image("measurement_plot.png", x=10, y=50, w=180)
pdf.output("report.pdf")
print("測定データとレポートが作成されました。")5. 演習問題
演習問題 1: データのフィッティングと統計量保存
ダミーデータを生成し、2次関数でフィッティングしてください。
フィッティング結果から得られるRMS(平均二乗誤差)を計算し、CSVファイルに保存してください。
解答例を表示
import numpy as np
from scipy.optimize import curve_fit
import pandas as pd
# 2次関数モデル(y = ax^2 + bx + c)
def quadratic_function(x, a, b, c):
return a * x**2 + b * x + c
# ダミーデータを生成
def generate_dummy_data(n_points=50, noise_level=1.0):
np.random.seed(42) # 乱数シードを固定
x = np.linspace(-10, 10, n_points) # 均一な範囲のx
true_a, true_b, true_c = 1.5, -2.0, 5.0 # 実際の2次関数の係数
y = true_a * x**2 + true_b * x + true_c # 実際の2次関数
noise = np.random.normal(0, noise_level, n_points) # ガウスノイズを追加
y_noisy = y + noise
return x, y_noisy, (true_a, true_b, true_c)
# フィッティングの実行
def fit_quadratic(x, y):
# 初期係数推定値(すべて0で初期化)
initial_guess = [1.0, 1.0, 1.0]
# curve_fitでフィッティング
params, _ = curve_fit(quadratic_function, x, y, p0=initial_guess)
return params
# RMS(平均二乗誤差)の計算
def calculate_rms(y_true, y_pred):
return np.sqrt(np.mean((y_true - y_pred) ** 2))
# CSVに結果を保存
def save_results_to_csv(filepath, rms, coefficients):
df = pd.DataFrame({
"Parameter": ["a", "b", "c", "RMS"],
"Value": list(coefficients) + [rms]
})
df.to_csv(filepath, index=False)
print(f"結果を {filepath} に保存しました。")
# メイン処理
def main():
# データの生成
x, y_noisy, true_coefficients = generate_dummy_data(100, 10)
# フィッティング
fitted_coefficients = fit_quadratic(x, y_noisy)
# フィッティング結果を用いて予測値生成
y_fitted = quadratic_function(x, *fitted_coefficients)
# RMS(平均二乗誤差)の計算
rms = calculate_rms(y_noisy, y_fitted)
print("フィッティング係数:", fitted_coefficients)
print("RMS:", rms)
# 結果をCSVに保存
save_results_to_csv("fitting_results.csv", rms, fitted_coefficients)
# データ表示(オプション、表示用)
try:
import matplotlib.pyplot as plt
plt.scatter(x, y_noisy, label="Noisy Data", color="blue")
plt.plot(x, y_fitted, label="Fitted Curve", color="red")
plt.legend()
plt.xlabel("x")
plt.ylabel("y")
plt.title("Quadratic Fit")
plt.show()
except ImportError:
print("matplotlibがインストールされていないため、プロットは表示されませんでした。")
# 実行
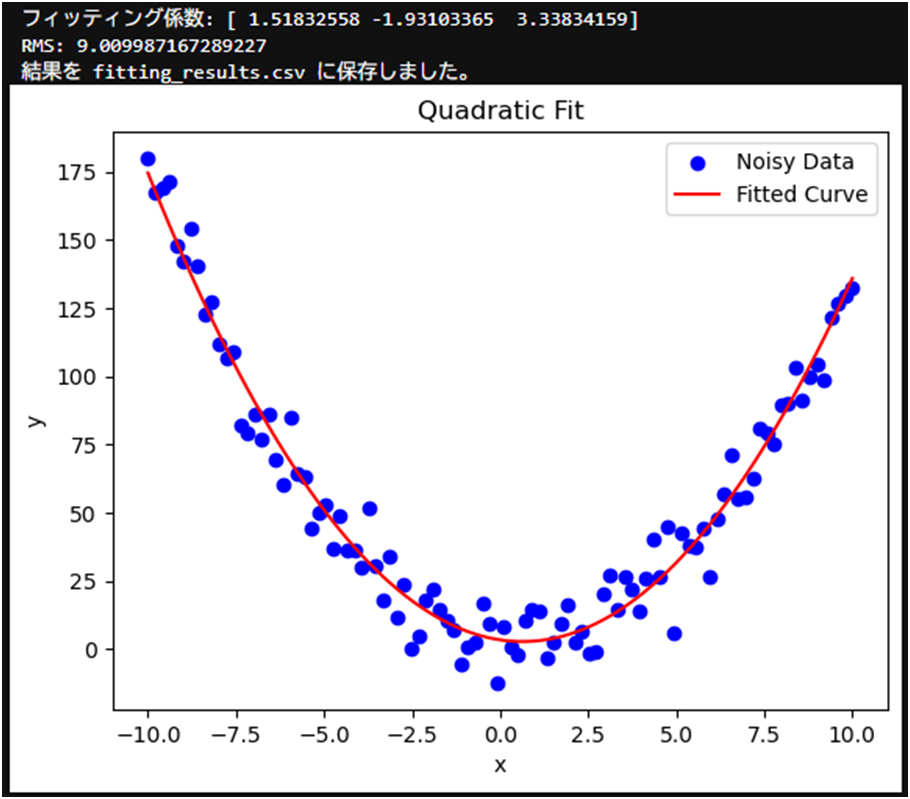
main()実行結果
演習問題 2: PDFレポートにコメントを追加
測定データとフィッティング結果を含むグラフをPDFレポートに追加してください。
レポート内に「考察」や「注釈」をコメントとして挿入してください。
解答例を表示
import numpy as np
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt
from reportlab.pdfgen import canvas
from reportlab.lib.pagesizes import letter
# 2次関数モデル(y = ax^2 + bx + c)
def quadratic_function(x, a, b, c):
return a * x**2 + b * x + c
# ダミーデータを生成
def generate_dummy_data(n_points=50, noise_level=1.0):
np.random.seed(42) # 乱数シードを固定
x = np.linspace(-10, 10, n_points)
true_a, true_b, true_c = 1.5, -2.0, 5.0 # 実際の2次関数の係数
y = true_a * x**2 + true_b * x + true_c
noise = np.random.normal(0, noise_level, n_points)
y_noisy = y + noise
return x, y_noisy, (true_a, true_b, true_c)
# フィッティングの実行
def fit_quadratic(x, y):
initial_guess = [1.0, 1.0, 1.0] # 初期値
params, _ = curve_fit(quadratic_function, x, y, p0=initial_guess)
return params
# RMS(平均二乗誤差)の計算
def calculate_rms(y_true, y_pred):
return np.sqrt(np.mean((y_true - y_pred)**2))
# グラフを保存
def save_plot(x, y_noisy, y_fitted, file_path="fit_plot.png"):
plt.scatter(x, y_noisy, color="blue", label="Noisy Data")
plt.plot(x, y_fitted, color="red", label="Fitted Curve")
plt.xlabel("x")
plt.ylabel("y")
plt.title("Quadratic Fit")
plt.legend()
plt.grid(True)
plt.savefig(file_path)
plt.close()
print(f"グラフを {file_path} に保存しました。")
# PDFレポートを作成
def create_pdf_report(pdf_path, coefficients, rms, plot_path, comments):
c = canvas.Canvas(pdf_path, pagesize=letter)
c.setFont("Helvetica", 12)
# タイトル
c.drawString(100, 750, "Quadratic Fitting Report")
c.setFont("Helvetica", 10)
# フィッティング結果
c.drawString(50, 700, "Fitted Coefficients:")
c.drawString(70, 680, f"a: {coefficients[0]:.4f}")
c.drawString(70, 660, f"b: {coefficients[1]:.4f}")
c.drawString(70, 640, f"c: {coefficients[2]:.4f}")
# RMS
c.drawString(50, 600, f"RMS (Root Mean Squared Error): {rms:.4f}")
# グラフを挿入
c.drawString(50, 560, "Fitting Plot:")
c.drawImage(plot_path, 50, 400, width=500, height=150)
# 考察・コメント
c.drawString(50, 350, "Comments:")
c.drawString(70, 330, comments)
# 最終出力
c.save()
print(f"PDFレポートが {pdf_path} に保存されました。")
# メイン処理
def main():
# ダミーデータ生成
x, y_noisy, true_coefficients = generate_dummy_data(100, 10)
# フィッティング
fitted_coefficients = fit_quadratic(x, y_noisy)
# フィッティング結果を使って予測値生成
y_fitted = quadratic_function(x, *fitted_coefficients)
# RMSの計算
rms = calculate_rms(y_noisy, y_fitted)
# フィッティング結果のログ
print("Fitted Coefficients:", fitted_coefficients)
print("RMS (Root Mean Squared Error):", rms)
# グラフ保存
plot_path = "fit_plot.png"
save_plot(x, y_noisy, y_fitted, plot_path)
# PDFレポート作成
comments = "This report demonstrates the result of fitting a quadratic function to noisy data. RMS provides an evaluation of the fitting accuracy."
pdf_path = "fitting_report.pdf"
create_pdf_report(pdf_path, fitted_coefficients, rms, plot_path, comments)
# 実行
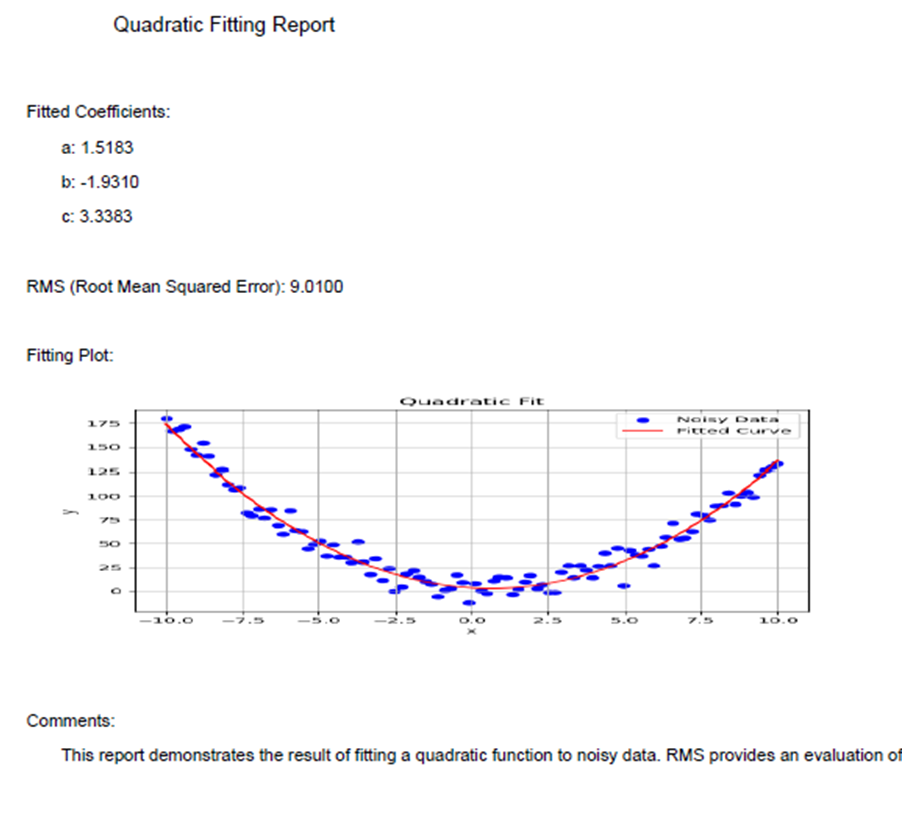
main()作成されたPDFファイルの内容
次回予告
次回(第9回)は、「計測器の自動化システム構築」を学びます。一連の測定、データ処理、レポート作成を自動化するシステムを構築し、効率的な運用方法を習得します!

