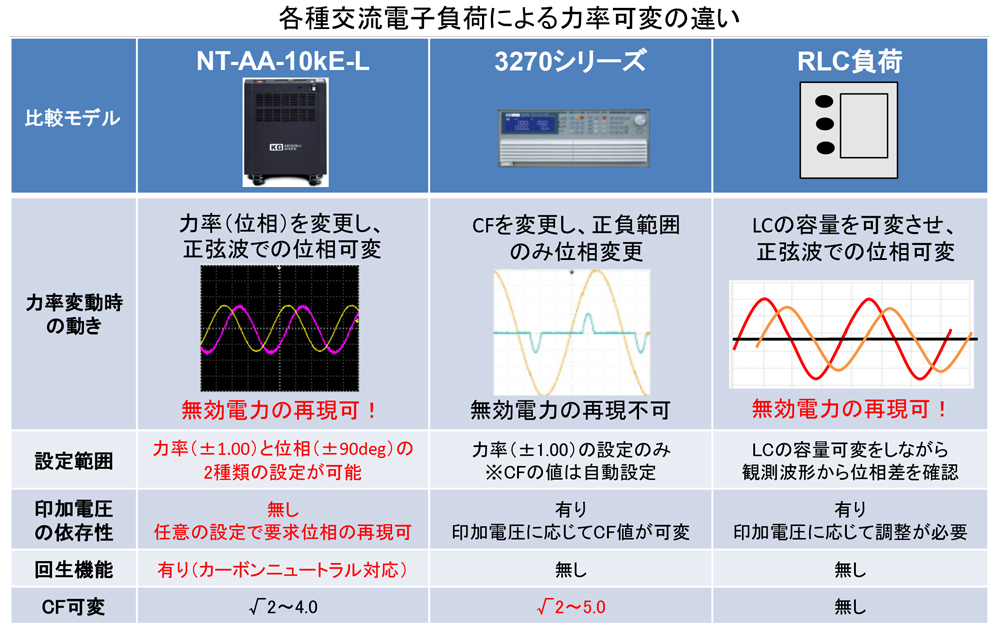
力率って、そもそもナニ？
力率とは
力率を一言で言うと、次のようになります。
「電源（発電所）から出力された電力が有効に使われている割合」
ということは、有効に使われない電力があるということになりますね。直流の場合、電力は１種類ですが、交流では３種類の電力があります。
| 電力 | 直流電力 | |
| 交流電力 | 皮相電力(S) | |
| 有効電力(P) | ||
| 無効電力(Q) | ||
冒頭の「電源から出力された電力」が「皮相電力（S）」であり、有効に使われている電力が「有効電力（P）」となります。
交流電力の定義
これらの３種類の交流電力は以下のように定義されています。
| 皮相電力（S） | 電源から出力された電力（電圧×電流） |
| 有効電力（P） | 負荷で実際に消費される（有効な）電力 |
| 無効電力（Q） | 負荷で消費されない（無効な）電力 |
そして、今回のテーマ「力率」は「電源から出力された電力が有効に使われている割合」 ですので、次のような式で表されます。
力率が低下するのはどんなとき？
力率の最大値は１であり、負荷が抵抗のときに１となります。負荷が抵抗ではないときに力率が低下するわけですが、ではどのような「からくり」で力率が低下するのでしょうか。最初に抵抗負荷の場合を見てみましょう。以下のように交流電源（V1）の出力に抵抗負荷（R1）が接続されている場合です。
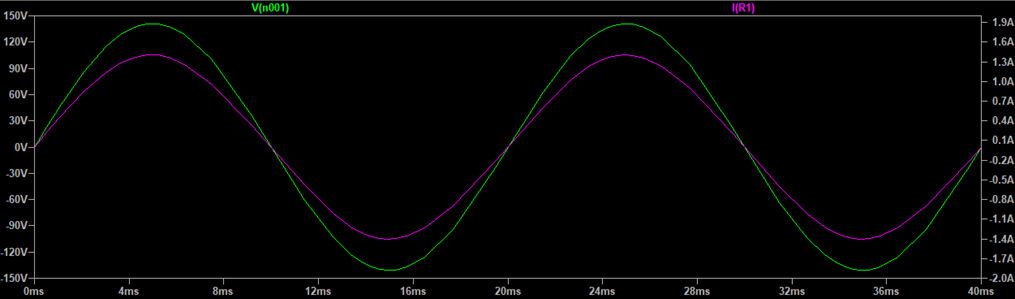
上記回路で抵抗R1に印加される電圧と流れる電流の波形ですが、電圧（緑色）が高くなるとそれに比例して電流（ピンク色）も増えていき、電圧が低くなると同様に電流も低下しています。
この結果は至極当たり前のように感じますが実は負荷に抵抗でない成分が含まれると、「当たり前」ではなくなります。
次の例は負荷にコイル（インダクタ）が含まれている場合で一般的には誘導性負荷と言います。下図のように抵抗負荷R1に直列でコイルL1が接続されています。
合わせて読みたい
このような場合の電圧・電流波形は以下のようになります。抵抗負荷のときと比較すると電流波形（ピンク色）の様子がだいぶ変わってきました。最初の山（ピーク）が電圧波形のそれよりも遅れています。
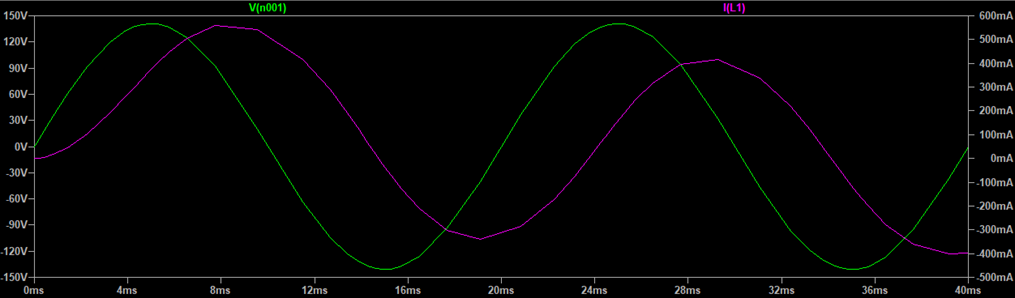
このような状態を「電流の位相が電圧よりも遅れている」と言います。では、なぜ電流の位相が電圧より遅れると力率が低下するのでしょうか。もう一度、力率の定義を思い出してみましょう。
「電源から出力された電力が有効に使われている割合」
抵抗負荷のときは、電圧が最大のときに電流も最大になっており、電力が有効に使われている（消費されている）ように見えますが、上記のように電流の位相が遅れている状態では電圧が最大のときに電流が低下、逆に電圧が最小のときに電流が上昇しており、とても有効に消費されているようには見えません。このときの有効電力を式で表すと次のようになり、力率はcosθで表されます。
有効電力（P）= 皮相電力 × 力率 = 皮相電力 × cosθ
cosθのθは電流の遅れ位相確度であり、θ=0度のときcosθ=1（力率最大）、θ=90度のときcosθ=0（力率最小）となります。（高校時代の三角関数が役に立ちました）
次の例は負荷にコンデンサ（キャパシタ）が含まれている場合で一般的に容量性負荷と言います。負荷抵抗R1に直列でコンデンサC1が接続されています。
合わせて読みたい
このような場合の電圧・電流波形の抵抗負荷のときとは異なりますが、コイルのときとは逆に電流波形のピークが電圧波形のそれよりも左側になっています。
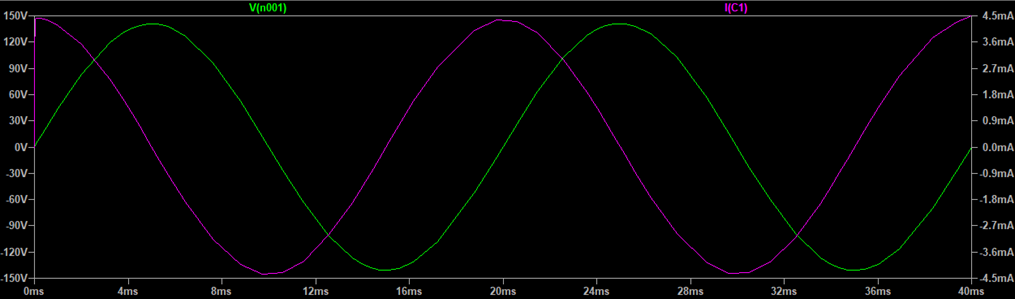
このような状態を「電流波形の位相が電圧波形よりも進んでいる」と言います。コイル（インダクタ）の場合は電流位相が遅れたことにより結果として力率が低下していました。これを「遅れ力率」と言います。これに対して、コンデンサ（キャパシタ）の場合は電流位相が進んでいるため「進み力率」と言います。さきほどの有効電力計算式に当てはめると
有効電力（P）= 皮相電力 × 力率 = 皮相電力 × cosθ
θ=0度のときに力率最大ということは変わりませんが、θ=-90度のときcosθ=0（力率最小）となります。
力率改善の必要性
力率が低いということは無効電力が大きく有効電力が少ないということですから、電源（発電所）から送られてきた電力を有効に消費できないことになります。このため発電所は力率が１であれば送らなくても済むはずの電力を供給することになり、また、高調波電流の増加による様々な弊害も発生する可能性があります。
このため、力率を出来る限り１に近づける「力率改善回路」は様々な機器に組み込まれています。
合わせて読みたい
関連ページ
交流電源 https://www.keisoku.co.jp/pw/product/power/ac/
交流電子負荷 https://www.keisoku.co.jp/pw/product/power/ac-load/
各種交流負荷における力率可変機能の挙動について https://www.keisoku.co.jp/pw/app/331/
